
生成有真实世界中的图的性质的图
真实世界中图的性质:
ThePowerLaw:真实世界中图的度分布多为幂律分布。即顶点的度是i的概率与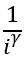 成正比。检查是否符合ThePowerLaw的方法通常是在log-log坐标下以横坐标为度,纵坐标为出现频率进行作图,观察是否近似符合一条直线。直观地说,真实图中有少量中心节点(称为集线器hub)连大量节点,而大部分节点的度很小。
成正比。检查是否符合ThePowerLaw的方法通常是在log-log坐标下以横坐标为度,纵坐标为出现频率进行作图,观察是否近似符合一条直线。直观地说,真实图中有少量中心节点(称为集线器hub)连大量节点,而大部分节点的度很小。
真实图的集聚系数较大。集聚系数(也称群聚系数、集群系数)是用来描述一个图中的顶点之间结集成团的程度的系数。具体来说,是一个点的邻接点之间相互连接的程度。在各类反映真实世界的网络结构,特别是社交网络结构中,各个结点之间倾向于形成密度相对较高的网群。
1、Erdos-Renyi模型:
ER随机图有两种构建方式:
(1)G(N,M),即先确定N个点,然后向这N个点之间撒M条边;
(2)G(N,p),先确定N个点,任意两个不同的节点之间的连边概率是p;
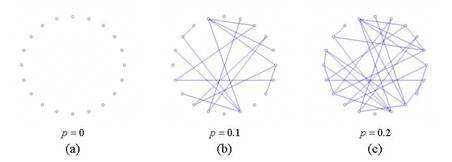
以第二种构建方式为例,生成的图类似下图。
用E-R模型生成的图的度分布为泊松分布,集聚系数低。没有前述真实图的性质。
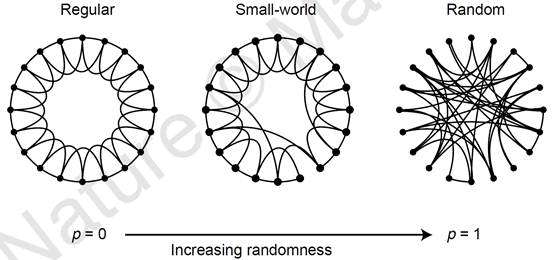
2、Watts-Strogatz模型:
第一步,给定一个含有 N 个点的图,把网络中所有节点编号为 1, 2, ..., N,把这些点环形排列。每个节点都与它左右相邻的各K/2个节点相连(K是偶数)。此时这是一个规则图。第二步,对这个规则图进行随机化重连:对于每个节点i,顺时针选取与节点i相连的 K/2 条边中的每一条边,边的一个端点仍然固定为节点i,以概率p随机选取网络中的任一个节点作为该条边的另一个端点。其中规定不得有重边和自环。在上述模型中,p=0 对应于完全规则网络,p=1 对应于完全随机网络。在WS小世界中每个节点的度至少是 K/2, 而在ER随机图中则无此限制。因此,即使在 p=1 的情况下,通过这种算法得到的WS小世界模型与相同节点,相同边数的ER随机图模型还是有区别的。由W-S模型生成的图,有局部聚类性质,但是会产生不切实际的度数分布(每个点都有≥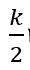 的度)。
的度)。
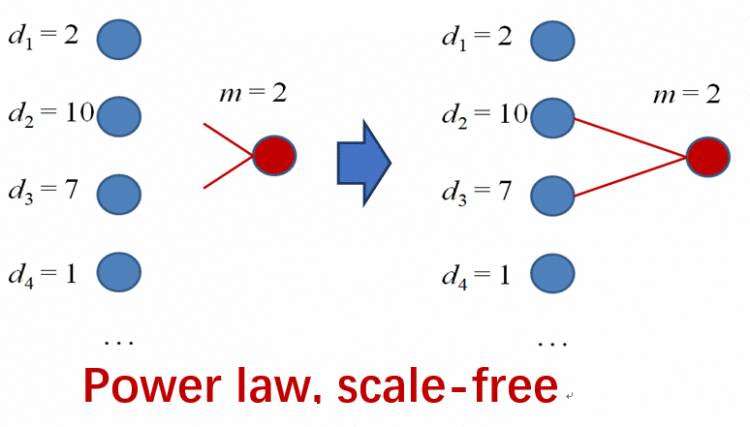
(二)优先连接(Preferential Attachment)模型
有两个关键特性:增长和优先连接。
优先连接(Preferential attachment)意味着节点之间的连接越多,接收新连接的可能性就越大。连接到顶点i的概率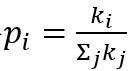 ,其中
,其中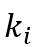 是i的度。这样,图中就会存在少量中心节点(称为集线器)连接大量新节点。
是i的度。这样,图中就会存在少量中心节点(称为集线器)连接大量新节点。
算法步骤如下:
第一步,初始化一个含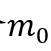 个顶点的随机图。
个顶点的随机图。
第二步,向图中添加一个新顶点,增加这个顶点和原图中m个顶点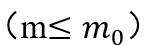 之间的边。和顶点i连边的概率
之间的边。和顶点i连边的概率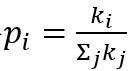 ,其中
,其中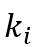 表示原图中顶点i的度。
表示原图中顶点i的度。
在每一个时间步,重复执行第二步,直到图的规模满足要求。
可以证明,这样生成的图的度分布满足幂律,图中有少量中心节点连接大量节点。这符合真实图(特别是社交网络图等)的性质。但B-A模型无法产生在实际网络中看到的高水平聚类。
1、R-MAT模型:
为了生成一个节点数为N的图,该模型建立一个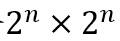 的邻接矩阵(如下图),其中
的邻接矩阵(如下图),其中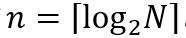 。同时,模型需要四个参数a,b,c,d,满足a+b+c+d=1且a≥max{b,c,d}。
。同时,模型需要四个参数a,b,c,d,满足a+b+c+d=1且a≥max{b,c,d}。
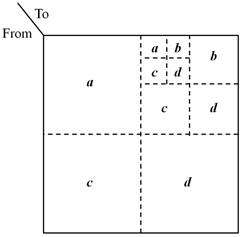
R-MAT模型生成图的步骤如下。
首先,初始化邻接矩阵中的元素为0。
为了生成包含N个点,E条边的图,模型递归的将矩阵分为四个等规模的部分(如上图所示),其中每一部分获得一条边的概率分别由四个参数决定。经过n次细分,模型即可定位到某个具体位置(i,j)并将其置1。模型反复递归插入边,直至达到边数目要求。
这个算法生成有向图。但对生成过程稍作修改模型即可生成无向图、带权图及二分图等。
这个模型刻画了真实图的度分布、小直径、重叠社区等一系列性质。
先给出矩阵的Kronecker积的定义。
给定矩阵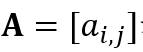 和B,大小分别为
和B,大小分别为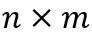 和
和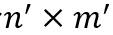 ,其Kronecker积为如下
,其Kronecker积为如下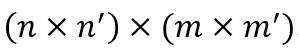 维矩阵。
维矩阵。
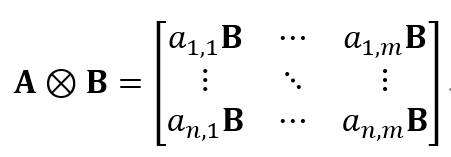
Kronecker图的生成需要给定一个包含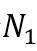 个节点、E_1条边的初始图
个节点、E_1条边的初始图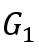 。
。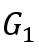 的k次Kronecker积
的k次Kronecker积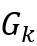 定义为
定义为

易观察到Kronecker图满足如下性质,其中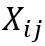 ,
,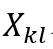 表示图G⊗H中的点,而
表示图G⊗H中的点,而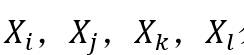 分别代表对应图G和H中的点。
分别代表对应图G和H中的点。
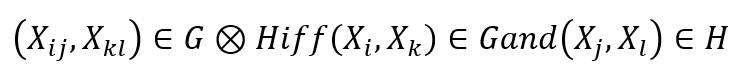
直观上,Kronecker图模型递归的构造了自相似(Self-similar)的图。图的从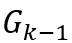 扩张到
扩张到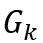 的过程,乃是把
的过程,乃是把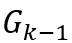 中的每个节点扩张(替换)成了一份G_1的拷贝(如下图)。
中的每个节点扩张(替换)成了一份G_1的拷贝(如下图)。
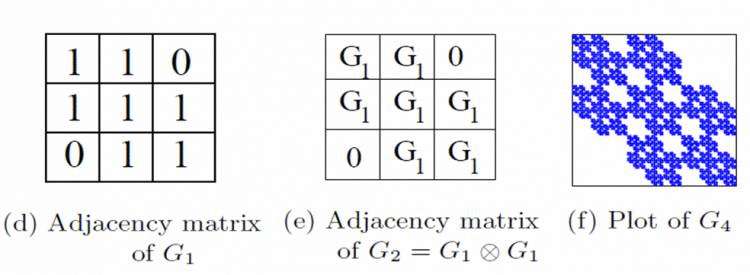
符合真实图的度分布、小直径等静态性质和稠密化(Densification)、直径收缩(Shrinking Diameter)等时序性质。
(四)Configurations Model
Aiello-Chung-Lu模型:
规定度分布要满足幂律分布,因此对于人为给定的参数α和β,规定
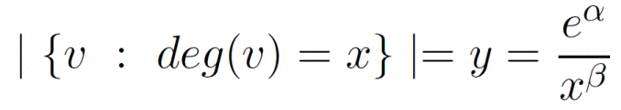
这样,生成的图就具有以下性质:
(1)最大的度是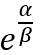
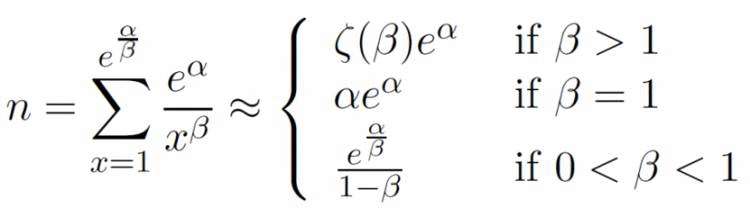
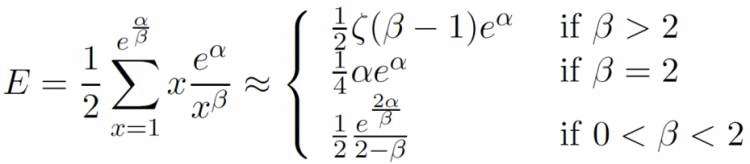
构造图的算法如下:
(1)建立集合L,对任意节点v,L包含deg(v)个该节点的独立拷贝(Distinct Copies);(2)在L的元素间选择一个随机匹配(Random Matching)即拷贝间的两两配对;(3)对两个节点u和v,它们之间的边数等于随机匹配中节点对应拷贝间的配对数。可见,ACL模型生成的图可能包括自环(Loop)和重边(Multi-edge),且很可能是非连通的。它的度分布严格满足幂律分布。
(五)Hyperbolic Graph Model
详见Krioukov D, Papadopoulos F, Kitsak M, et al. Hyperbolic geometry of complex networks[J]. Physical Review E, 2010, 82(3): 036106.本文由于篇幅限制不讨论。
(六)Stochastic Block model
详见Airoldi E M, Blei D M, Fienberg S E, et al. Mixed membership stochastic blockmodels[J]. Journal of machine learning research, 2008, 9(Sep): 1981-2014.本文由于篇幅限制不讨论。
1、DeepGMG
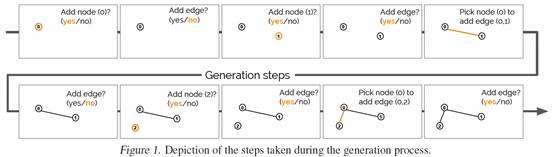
如下图,DeepGMG将图生成的过程建模成了(1)决定是否在现有图上增加顶点(2)决定是否在新增节点上增加边 (3)决定在新增节点和哪个节点之间加边三个部分所组成的序列。
如下图,把上述三个过程分别建模成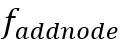 (是否加顶点),
(是否加顶点),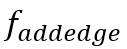 (是否加边),
(是否加边),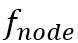 (加哪条边)三个函数。三个函数都由多层神经网络实现。每一步迭代过程中,先判断是否要继续加顶点(
(加哪条边)三个函数。三个函数都由多层神经网络实现。每一步迭代过程中,先判断是否要继续加顶点(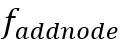 ),然后判断是否加边(
),然后判断是否加边(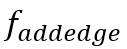 ),要的话加哪条边
),要的话加哪条边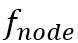 。直到
。直到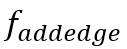 为false时停止在新增节点上加边,而迭代到
为false时停止在新增节点上加边,而迭代到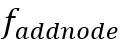 为false时,图生成结束。
为false时,图生成结束。

如下图,A表示顶点数为n的图的邻接矩阵,E是表示边的属性的张量,F是表示顶点属性的矩阵。GraphVAE采用了和VAE类似的结构,encoder将图的信息G = (A, E, F) 转换为近似符合正态分布的向量z,再由decoder将z转换为G ̃。
Loss函数包含
(1)向量z分布与正态分布之间的相似性
(2)生成的G ̃和原图G之间的相似性两个部分。
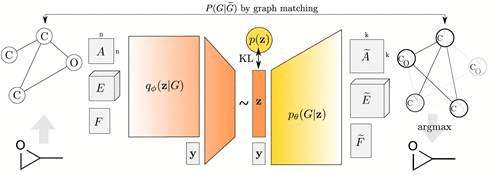
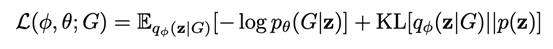
3、GraphRNN
将图的生成处理成点和连边序列的生成。
如下图,共有两个RNN ( graph-level RNN和 edge-level RNN ) 参与图生成。绿色箭头表示graph-levelRNN,它的 表示图的当前状态的编码。蓝色箭头表示edge-level RNN,它的
表示图的当前状态的编码。蓝色箭头表示edge-level RNN,它的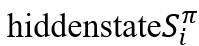 表示新加入的节点i和旧图中其他节点的连边与否。每次更新时,
表示新加入的节点i和旧图中其他节点的连边与否。每次更新时,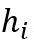 用来初始化edge-level RNN,而edge-level RNN的输出
用来初始化edge-level RNN,而edge-level RNN的输出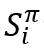 和当前
和当前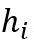 则作为下一个graph-level RNN hiddenstate的输入。
则作为下一个graph-level RNN hiddenstate的输入。
这样,每一步生成一个新节点(graph-level RNN)和这个点与其他node之间的连边(edge-level RNN)。
GraphRNN具有自回归结构,生成的图可以不受图顶点数目的限制。
为了降低模型的时间复杂度,graphRNN按BreathFirstSearch顺序生成节点。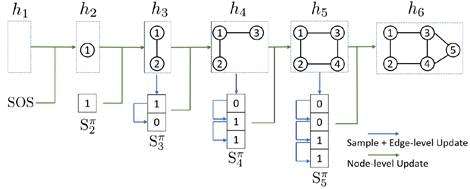
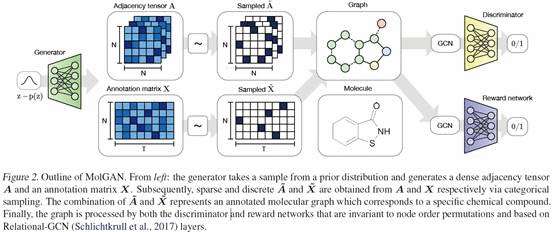
4、MolGAN
如下图,MolGAN是生成分子结构图的神经网络。它的结构类似于GAN,从先验分布中采样,作为generator的输入,输出邻接矩阵A(包含边的类型信息)和注释矩阵X(代表每个节点对应的原子类型)。A和X是连续而密集的矩阵(A和X中的值是0和1之间的连续量,代表概率)。经过分类采样得到离散稀疏的A ̃和X ̃矩阵。将生成的图输入discriminator(评判这个化合物是否合理)和rewardnetwork(评判化合物是否具有某些想要的性质,比如可溶于水),进行评判。
由于离散化A和X的过程是不可求导的,论文中采用了三种不同的方法来决定discriminator和rewardnetwork的输入(因为篇幅限制,略去)。
5、传统和基于深度学习的算法的比较
人为观察到真实图一些重要的性质,并依此构造算法。
可以生成大规模图
易于理解,有丰富数学基础
基于深度学习的算法:
从数据集中的真实图中学习。
能从数据集中同时捕捉到结构和属性信息
对数据集中图的拟合更好
6、实验结果:
我们使用You J, Ying R, Ren X, et al. Graphrnn: Generating realistic graphs with deep auto-regressive models[J]. arXiv preprint arXiv:1802.08773, 2018.这篇文章中的指标和数据来分析实验结果。
对于每个图集合,我们有集合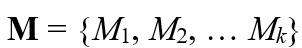 , 其中
, 其中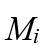 是图的衡量指标。Mi是单变量的实数集上的分布,比如集聚系数分布,度分布等。
是图的衡量指标。Mi是单变量的实数集上的分布,比如集聚系数分布,度分布等。
用Wasserstein distance作为衡量两个分布之间距离的指标:
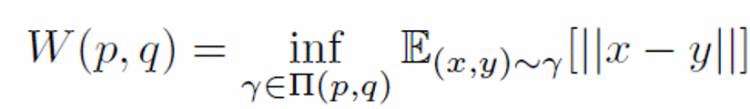
接下来介绍Maximum Mean Discrepancy (MMD) measures。
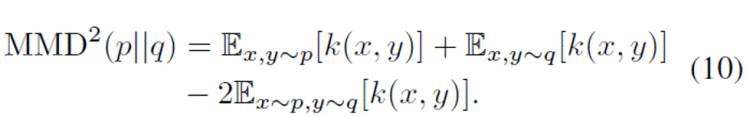
其中k是kernel函数。
我们用下图公式作为kernel函数:
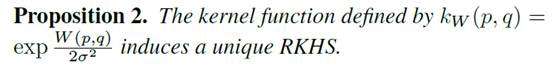
这样,我们就能得到生成模型生成的图和真实图集合之间的差距,从而评价衡量指标。
2、数据集
500个双社区图,顶点数目在60到160之间。每个团是由E-R模型按n = |V|/2 和p = 0.3生成的。我们在两个团的节点之间共等概率加了0.05|V |条边。
(2)Grid.
100个标准二维网格图,顶点数目在100到400之间。
(3)B-A.
500 graphs with 100 ≤ |V | ≤ 200 that are generated using the Baraba ́si-Albert model. During generation, each node is connected to 4 existing nodes.
(4)Protein.
918 个蛋白质结构图 (Dobson & Doig, 2003),顶点数目在100到500之间。顶点代表氨基酸,如果两个氨基酸之间距离小于6埃(Angstrom),那么对应的两个顶点之间有连边。
从Citeseer上下载的757个3-hop Ego网络(Sen et al., 2008),顶点数目在50和399之间。顶点表示文章,边表示引用关系。
3、实验结果
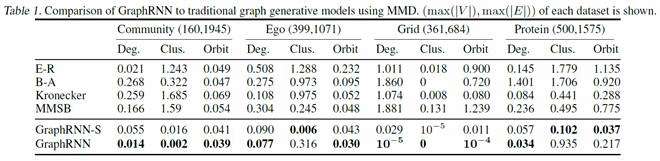
下图(table1)表示以MMD为指标,对一些传统图生成模型和GraphRNN的结果比较。
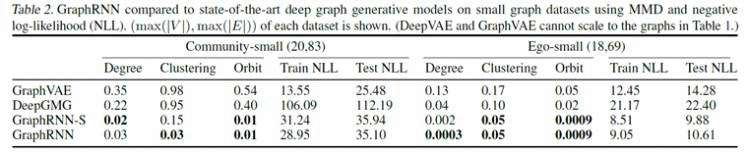
下图(table 2)表示以MMD和NLL为指标,对于各类learning-based图生成模型的实验结果比较。
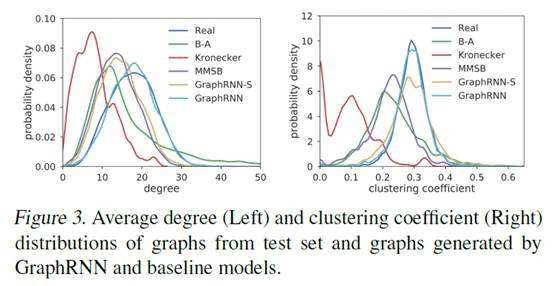
下图表示各类图生成模型生成的图和真实图的度分布、集聚系数分布的比较。
Reference:
1. [GraphVAE]Simonovsky, Martin, and Nikos Komodakis. "Graphvae: Towards generation ofsmall graphs using variational autoencoders." InternationalConference on Artificial Neural Networks. Springer, Cham, 2018.
2. [MolGAN] De Cao,Nicola, and Thomas Kipf. "MolGAN: An implicit generative model for smallmolecular graphs." arXiv preprint arXiv:1805.11973 (2018).
3. [GraphRNN] You,Jiaxuan, et al. "Graphrnn: Generating realistic graphs with deepauto-regressive models." arXiv preprint arXiv:1802.08773 (2018).
4. [BiGG] Dai,Hanjun, et al. "Scalable Deep Generative Modeling for SparseGraphs." In ICML 2020.
5. William L.Hamilton, Graph Rrepresentation Learning, Chapter 8-9.
6. Guo, Xiaojie, andLiang Zhao. “A Systematic Survey on Deep Generative Models for GraphGeneration.” arXiv preprint arXiv:2007.06686 (2020).
7. Krioukov D,Papadopoulos F, Kitsak M, et al. Hyperbolic geometry of complex networks[J].Physical Review E, 2010, 82(3): 036106.
8. Airoldi E M, BleiD M, Fienberg S E, et al. Mixed membership stochastic blockmodels[J]. Journalof machine learning research, 2008, 9(Sep): 1981-2014.
9. Erdős P, Rényi A.On the evolution of random graphs[J]. Publ. Math. Inst. Hung. Acad. Sci, 1960,5(1): 17-60.
10. William Aiello,Fan Chung, Linyuan Lu "A random graph model for power law graphs,"Experimental Mathematics, Experiment. Math. 10(1), 53-66, (2001)
11. Leskovec, Jure;Chakrabarti, Deepayan; Kleinberg, Jon; Faloutsos, Christos; Ghahramani,Zoubin (2010), "Kroneckergraphs: an approach to modeling networks", Journalof Machine Learning Research, 11:985–1042, arXiv:0812.4905, Bibcode:2008arXiv0812.4905L, MR 2600637.
12. Chakrabarti,Deepayan& Zhan, Yiping &Faloutsos, Christos. (2004). R-MAT: A recursivemodel for graph mining. SIAM Proceedings Series. 6. 10.1137/1.9781611972740.43.
13. Watts, D. J.; Strogatz, S. H. (1998). "Collective dynamics of 'small-world' networks" (PDF) . Nature . 393 (6684): 440–442. Bibcode:1998Natur.393..440W. doi:10.1038/30918. PMID 9623998.